
Polynomial functions. More...
#include <itpp/base/itcompat.h>#include <itpp/signal/poly.h>#include <itpp/base/converters.h>#include <itpp/base/algebra/eigen.h>#include <itpp/base/specmat.h>#include <itpp/base/matfunc.h>Go to the source code of this file.
Namespaces | |
| namespace | itpp |
| itpp namespace | |
Functions | |
| double | itpp::cheb (int n, double x) |
| Chebyshev polynomial of the first kindChebyshev polynomials of the first kind can be defined as follows:
| |
| vec | itpp::cheb (int n, const vec &x) |
| Chebyshev polynomial of the first kindChebyshev polynomials of the first kind can be defined as follows:
| |
| mat | itpp::cheb (int n, const mat &x) |
| Chebyshev polynomial of the first kindChebyshev polynomials of the first kind can be defined as follows:
| |
| void | itpp::poly (const vec &r, vec &p) |
Create a polynomial of the given rootsCreate a polynomial p with roots r. | |
| void | itpp::poly (const cvec &r, cvec &p) |
Create a polynomial of the given rootsCreate a polynomial p with roots r. | |
| void | itpp::roots (const vec &p, cvec &r) |
Calculate the roots of the polynomialCalculate the roots r of the polynomial p. | |
| void | itpp::roots (const cvec &p, cvec &r) |
Calculate the roots of the polynomialCalculate the roots r of the polynomial p. | |
| vec | itpp::polyval (const vec &p, const vec &x) |
Evaluate polynomialEvaluate the polynomial p (of length 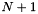 at the points at the points x The output is given by
. | |
| cvec | itpp::polyval (const vec &p, const cvec &x) |
Evaluate polynomialEvaluate the polynomial p (of length 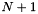 at the points at the points x The output is given by
. | |
| cvec | itpp::polyval (const cvec &p, const vec &x) |
Evaluate polynomialEvaluate the polynomial p (of length 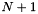 at the points at the points x The output is given by
. | |
| cvec | itpp::polyval (const cvec &p, const cvec &x) |
Evaluate polynomialEvaluate the polynomial p (of length 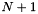 at the points at the points x The output is given by
. | |
Polynomial functions.
Copyright (C) 1995-2010 (see AUTHORS file for a list of contributors)
This file is part of IT++ - a C++ library of mathematical, signal processing, speech processing, and communications classes and functions.
IT++ is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.
IT++ is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
You should have received a copy of the GNU General Public License along with IT++. If not, see http://www.gnu.org/licenses/.
Definition in file poly.cpp.
Generated on Sat Jul 6 2013 10:54:27 for IT++ by Doxygen 1.8.2