A Reed-Solomon code is a 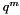 -ary BCH code of length
-ary BCH code of length 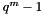 . The generator polynomial for a
. The generator polynomial for a 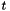 -error correcting code is
-error correcting code is 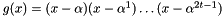 . The decoder uses the Berlkamp-Massey algorithm for decoding as described in: S. B. Wicker, "Error Control Systems for digital communication and storage," Prentice Hall. The following example simulates a binary (i.e.
. The decoder uses the Berlkamp-Massey algorithm for decoding as described in: S. B. Wicker, "Error Control Systems for digital communication and storage," Prentice Hall. The following example simulates a binary (i.e. 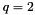 ) Reed-Solomon code with parameters
) Reed-Solomon code with parameters 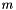 and
and 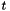 :
:
using namespace itpp;
using std::cout;
using std::endl;
int main()
{
int m, t, n, k, q, NumBits, NumCodeWords;
double p;
bvec uncoded_bits, coded_bits, received_bits, decoded_bits;
NumCodeWords = 1000;
p = 0.01;
m = 3;
t = 2;
cout << "Number of Reed-Solomon code-words to simulate: " << NumCodeWords << endl;
cout << "BSC Error probability : " << p << endl;
cout << "RS m: " << m << endl;
cout << "RS t: " << t << endl;
cout << "Simulating an Reed-Solomon code with the following parameters:" << endl;
cout << "n = " << n << endl;
cout << "k = " << k << endl;
cout << "q = " << q << endl;
NumBits = m * k * NumCodeWords;
uncoded_bits =
randb(NumBits);
coded_bits = reed_solomon.encode(uncoded_bits);
received_bits = bsc(coded_bits);
decoded_bits = reed_solomon.decode(received_bits);
berc.
count(uncoded_bits, decoded_bits);
cout <<
"The bit error probability after decoding is " << berc.
get_errorrate() << endl;
return 0;
}
A typical run of this program can look like this:
Number of Reed-Solomon code-words
to simulate: 1000
BSC Error probability : 0.01
RS m: 3
RS t: 2
Simulating an Reed-Solomon code with the following parameters:
n = 7
k = 3
q = 8
The bit error probability after decoding is 0.000333333

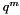 -ary BCH code of length
-ary BCH code of length 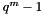 . The generator polynomial for a
. The generator polynomial for a 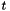 -error correcting code is
-error correcting code is 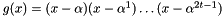 . The decoder uses the Berlkamp-Massey algorithm for decoding as described in: S. B. Wicker, "Error Control Systems for digital communication and storage," Prentice Hall. The following example simulates a binary (i.e.
. The decoder uses the Berlkamp-Massey algorithm for decoding as described in: S. B. Wicker, "Error Control Systems for digital communication and storage," Prentice Hall. The following example simulates a binary (i.e. 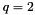 ) Reed-Solomon code with parameters
) Reed-Solomon code with parameters 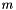 and
and 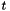 :
: