Functions
double	itpp::besselj (int nu, double x)
	Bessel function of first kind of order nu for nu integer.

vec	itpp::besselj (int nu, const vec &x)
	Bessel function of first kind of order nu for nu integer.

double	itpp::besselj (double nu, double x)
	Bessel function of first kind of order nu. nu is real.

vec	itpp::besselj (double nu, const vec &x)
	Bessel function of first kind of order nu. nu is real.

double	itpp::bessely (int nu, double x)
	Bessel function of second kind of order nu. nu is integer.

vec	itpp::bessely (int nu, const vec &x)
	Bessel function of second kind of order nu. nu is integer.

double	itpp::bessely (double nu, double x)
	Bessel function of second kind of order nu. nu is real.

vec	itpp::bessely (double nu, const vec &x)
	Bessel function of second kind of order nu. nu is real.

double	itpp::besseli (double nu, double x)
	Modified Bessel function of first kind of order nu. nu is double. x is double.

vec	itpp::besseli (double nu, const vec &x)
	Modified Bessel function of first kind of order nu. nu is double. x is double.

double	itpp::besselk (int nu, double x)
	Modified Bessel function of second kind of order nu. nu is double. x is double.

vec	itpp::besselk (int nu, const vec &x)
	Modified Bessel function of second kind of order nu. nu is double. x is double.

Detailed Description

end of math group

Function Documentation

ITPP_EXPORT double itpp::besselj	(	int	nu,
		double	x
	)

Bessel function of first kind of order nu for nu integer.

The bessel function of first kind is defined as:

$J_{\nu}(x) = \sum_{k=0}^{\infty} \frac{ (-1)^{k} }{k! \Gamma(\nu+k+1) } \left(\frac{x}{2}\right)^{\nu+2k}$

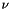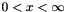where $\nu$ is the order and $0 < x < \infty$ .

Definition at line 44 of file bessel.cpp.

ITPP_EXPORT double itpp::bessely	(	int	nu,
		double	x
	)

Bessel function of second kind of order nu. nu is integer.

The Bessel function of second kind is defined as:

$Y_{\nu}(x) = \frac{J_{\nu}(x) \cos(\nu\pi) - J_{-\nu}(x)}{\sin(\nu\pi)}$

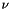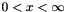where $\nu$ is the order and $0 < x < \infty$ .

Definition at line 68 of file bessel.cpp.

ITPP_EXPORT double itpp::besseli	(	double	nu,
		double	x
	)

Modified Bessel function of first kind of order nu. nu is double. x is double.

The Modified Bessel function of first kind is defined as:

$I_{\nu}(x) = i^{-\nu} J_{\nu}(ix)$

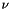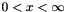where $\nu$ is the order and $0 < x < \infty$ .

Definition at line 91 of file bessel.cpp.

ITPP_EXPORT double itpp::besselk	(	int	nu,
		double	x
	)

Modified Bessel function of second kind of order nu. nu is double. x is double.

The Modified Bessel function of second kind is defined as:

$K_{\nu}(x) = \frac{\pi}{2} i^{\nu+1} [J_{\nu}(ix) + i Y_{\nu}(ix)]$

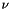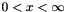where $\nu$ is the order and $0 < x < \infty$ .

Definition at line 103 of file bessel.cpp.