
Functions on vectors and matrices. More...
Functions | |
| template<class T > | |
| int | itpp::length (const Vec< T > &v) |
| Length of vector. | |
| template<class T > | |
| int | itpp::size (const Vec< T > &v) |
| Length of vector. | |
| template<class T > | |
| T | itpp::sum (const Vec< T > &v) |
| Sum of all elements in the vector. | |
| template<class T > | |
| Vec< T > | itpp::sum (const Mat< T > &m, int dim=1) |
Sum of elements in the matrix m, either along columns or rows. | |
| template<class T > | |
| T | itpp::sumsum (const Mat< T > &X) |
| Sum of all elements in the given matrix. Fast version of sum(sum(X)) | |
| template<class T > | |
| T | itpp::sum_sqr (const Vec< T > &v) |
| Sum of square of the elements in a vector. | |
| template<class T > | |
| Vec< T > | itpp::sum_sqr (const Mat< T > &m, int dim=1) |
Sum of the square of elements in the matrix m. | |
| template<class T > | |
| Vec< T > | itpp::cumsum (const Vec< T > &v) |
| Cumulative sum of all elements in the vector. | |
| template<class T > | |
| Mat< T > | itpp::cumsum (const Mat< T > &m, int dim=1) |
Cumulative sum of elements in the matrix m. | |
| template<class T > | |
| T | itpp::prod (const Vec< T > &v) |
| The product of all elements in the vector. | |
| template<class T > | |
| Vec< T > | itpp::prod (const Mat< T > &m, int dim=1) |
Product of elements in the matrix m. | |
| template<class T > | |
| Vec< T > | itpp::cross (const Vec< T > &v1, const Vec< T > &v2) |
| Vector cross product. Vectors need to be of size 3. | |
| template<class T > | |
| Vec< T > | itpp::zero_pad (const Vec< T > &v, int n) |
| Zero-pad a vector to size n. | |
| template<class T > | |
| Vec< T > | itpp::zero_pad (const Vec< T > &v) |
| Zero-pad a vector to the nearest greater power of two. | |
| template<class T > | |
| Mat< T > | itpp::zero_pad (const Mat< T > &m, int rows, int cols) |
| Zero-pad a matrix to size rows x cols. | |
| template<class T > | |
| T | itpp::index_zero_pad (const Vec< T > &v, const int index) |
| template<class T > | |
| void | itpp::transpose (const Mat< T > &m, Mat< T > &out) |
Transposition of the matrix m returning the transposed matrix in out. | |
| template<class T > | |
| Mat< T > | itpp::transpose (const Mat< T > &m) |
Transposition of the matrix m. | |
| template<class T > | |
| void | itpp::hermitian_transpose (const Mat< T > &m, Mat< T > &out) |
| template<class T > | |
| Mat< T > | itpp::hermitian_transpose (const Mat< T > &m) |
Hermitian transpose (complex conjugate transpose) of the matrix m. | |
| template<class Num_T > | |
| bool | itpp::is_hermitian (const Mat< Num_T > &X) |
Returns true if matrix X is hermitian, false otherwise. | |
| template<class Num_T > | |
| bool | itpp::is_unitary (const Mat< Num_T > &X) |
Returns true if matrix X is unitary, false otherwise. | |
| template<class Num_T > | |
| Mat< Num_T > | itpp::kron (const Mat< Num_T > &X, const Mat< Num_T > &Y) |
| Computes the Kronecker product of two matrices. | |
| ITPP_EXPORT cmat | itpp::sqrtm (const cmat &A) |
Square root of the complex square matrix A. | |
| ITPP_EXPORT cmat | itpp::sqrtm (const mat &A) |
Square root of the real square matrix A. | |
| template<class T > | |
| int | itpp::rank (const Mat< T > &m, double tol=-1.0) |
Calculate the rank of matrix m. | |
| template<> | |
| int | itpp::rank (const imat &m, double tol) |
| Specialisation of rank() function. | |
| template<> | |
| int | itpp::rank (const smat &m, double tol) |
| Specialisation of rank() function. | |
| template<> | |
| int | itpp::rank (const bmat &, double) |
| Specialisation of rank() function. | |
| template<class T > | |
| Vec< T > | repmat (const Vec< T > &v, int n) |
Creates a vector with n copies of the vector v. | |
| template<class T > | |
| Mat< T > | repmat (const Mat< T > &data, int m, int n) |
Creates a matrix with m by n copies of the matrix data. | |
| template<class T > | |
| Mat< T > | repmat (const Vec< T > &v, int m, int n, bool transpose=false) |
Returns a matrix with m by n copies of the vector data. | |
Functions on vectors and matrices.
| Vec<T> itpp::sum | ( | const Mat< T > & | m, |
| int | dim = 1 |
||
| ) |
Sum of elements in the matrix m, either along columns or rows.
sum(m) = sum(m, 1) returns a vector where the elements are sum over each column, whereas sum(m, 2) returns a vector where the elements are sum over each row.
Definition at line 77 of file matfunc.h.
References itpp::Mat< Num_T >::cols(), itpp::Mat< Num_T >::get_col(), itpp::Mat< Num_T >::get_row(), it_assert, itpp::Mat< Num_T >::rows(), itpp::Vec< Num_T >::set_size(), and itpp::sum().
| Vec<T> itpp::sum_sqr | ( | const Mat< T > & | m, |
| int | dim = 1 |
||
| ) |
Sum of the square of elements in the matrix m.
sum(m) = sum(m, 1) returns a vector where the elements are sum squared over each column, whereas sum(m, 2) returns a vector where the elements are sum squared over each row
Definition at line 134 of file matfunc.h.
References itpp::Mat< Num_T >::cols(), itpp::Mat< Num_T >::get_col(), itpp::Mat< Num_T >::get_row(), it_assert, itpp::Mat< Num_T >::rows(), itpp::Vec< Num_T >::set_size(), and itpp::sum_sqr().
| Mat<T> itpp::cumsum | ( | const Mat< T > & | m, |
| int | dim = 1 |
||
| ) |
Cumulative sum of elements in the matrix m.
cumsum(m) = cumsum(m, 1) returns a matrix where the elements are sums over each column, whereas cumsum(m, 2) returns a matrix where the elements are sums over each row
Definition at line 176 of file matfunc.h.
References itpp::Mat< Num_T >::cols(), itpp::cumsum(), itpp::Mat< Num_T >::get_col(), itpp::Mat< Num_T >::get_row(), it_assert, itpp::Mat< Num_T >::rows(), and itpp::Mat< Num_T >::set_col().
| Vec<T> itpp::prod | ( | const Mat< T > & | m, |
| int | dim = 1 |
||
| ) |
Product of elements in the matrix m.
prod(m) = prod(m, 1) returns a vector where the elements are products over each column, whereas prod(m, 2) returns a vector where the elements are products over each row
Definition at line 214 of file matfunc.h.
References itpp::Mat< Num_T >::cols(), itpp::Mat< Num_T >::get_col(), itpp::Mat< Num_T >::get_row(), it_assert, itpp::prod(), and itpp::Mat< Num_T >::rows().
| T itpp::index_zero_pad | ( | const Vec< T > & | v, |
| const int | index | ||
| ) |
Return zero if indexing outside the vector v otherwise return the element index
Definition at line 297 of file matfunc.h.
References itpp::Vec< Num_T >::size().
Referenced by itpp::xcorr_old().
| void itpp::hermitian_transpose | ( | const Mat< T > & | m, |
| Mat< T > & | out | ||
| ) |
Hermitian transpose (complex conjugate transpose) of the matrix m returning the transposed matrix in out
Definition at line 318 of file matfunc.h.
References itpp::Mat< Num_T >::H().
| bool itpp::is_hermitian | ( | const Mat< Num_T > & | X | ) |
Returns true if matrix X is hermitian, false otherwise.
A square matrix 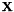 is hermitian if
is hermitian if
![\[ \mathbf{X} = \mathbf{X}^H \]](form_7.png)
Definition at line 336 of file matfunc.h.
References itpp::Mat< Num_T >::H().
| bool itpp::is_unitary | ( | const Mat< Num_T > & | X | ) |
Returns true if matrix X is unitary, false otherwise.
A square matrix 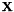 is unitary if
is unitary if
![\[ \mathbf{X}^H = \mathbf{X}^{-1} \]](form_8.png)
Definition at line 355 of file matfunc.h.
References itpp::Mat< Num_T >::H(), and itpp::inv().
| Mat<Num_T> itpp::kron | ( | const Mat< Num_T > & | X, |
| const Mat< Num_T > & | Y | ||
| ) |
Computes the Kronecker product of two matrices.
K = kron(X, Y) returns the Kronecker tensor product of X and Y. The result is a large array formed by taking all possible products between the elements of X and those of Y. If X is (m x n) and Y is (p x q), then kron(X, Y) is (m*p x n*q).
Definition at line 443 of file matfunc.h.
References itpp::Mat< Num_T >::cols(), itpp::Mat< Num_T >::rows(), and itpp::Mat< Num_T >::set_submatrix().
| ITPP_EXPORT cmat itpp::sqrtm | ( | const cmat & | A | ) |
Square root of the complex square matrix A.
This function computes the matrix square root of the complex square matrix A. The implementation is based on the Matlab/Octave sqrtm() function.
Ref: N. J. Higham, "Numerical Analysis Report No. 336", Manchester Centre for Computational Mathematics, Manchester, England, January 1999
| ITPP_EXPORT cmat itpp::sqrtm | ( | const mat & | A | ) |
Square root of the real square matrix A.
This function computes the matrix square root of the real square matrix A. Please note that the returned matrix is complex. The implementation is based on the Matlab/Octave sqrtm() function.
Ref: N. J. Higham, "Numerical Analysis Report No. 336", Manchester Centre for Computational Mathematics, Manchester, England, January 1999
| int itpp::rank | ( | const Mat< T > & | m, |
| double | tol = -1.0 |
||
| ) |
Calculate the rank of matrix m.
| m | Input matrix |
| tol | Tolerance used for comparing the singular values with zero. If negative, it is automatically determined. |
Definition at line 493 of file matfunc.h.
References itpp::Mat< Num_T >::cols(), itpp::eps, itpp::Mat< Num_T >::rows(), and itpp::svd().
Referenced by itpp::GF2mat::inverse(), itpp::rank(), and itpp::GF2mat::row_rank().
|
related |
|
related |
|
related |
Returns a matrix with m by n copies of the vector data.
| v | Vector to be repeated |
| m | Number of times to repeat data vertically |
| n | Number of times to repeat data horizontally |
| transpose | Specifies the input vector orientation (column vector by default) |
Definition at line 425 of file matfunc.h.
References itpp::transpose().
Generated on Sat May 25 2013 16:32:27 for IT++ by Doxygen 1.8.2