
Functions | |
| double | itpp::cheb (int n, double x) |
| Chebyshev polynomial of the first kindChebyshev polynomials of the first kind can be defined as follows:
| |
| vec | itpp::cheb (int n, const vec &x) |
| Chebyshev polynomial of the first kindChebyshev polynomials of the first kind can be defined as follows:
| |
| mat | itpp::cheb (int n, const mat &x) |
| Chebyshev polynomial of the first kindChebyshev polynomials of the first kind can be defined as follows:
| |
| void | itpp::poly (const vec &r, vec &p) |
Create a polynomial of the given rootsCreate a polynomial p with roots r. | |
| void | itpp::poly (const cvec &r, cvec &p) |
Create a polynomial of the given rootsCreate a polynomial p with roots r. | |
| vec | itpp::poly (const vec &r) |
Create a polynomial of the given rootsCreate a polynomial p with roots r. | |
| cvec | itpp::poly (const cvec &r) |
Create a polynomial of the given rootsCreate a polynomial p with roots r. | |
| void | itpp::roots (const vec &p, cvec &r) |
Calculate the roots of the polynomialCalculate the roots r of the polynomial p. | |
| void | itpp::roots (const cvec &p, cvec &r) |
Calculate the roots of the polynomialCalculate the roots r of the polynomial p. | |
| cvec | itpp::roots (const vec &p) |
Calculate the roots of the polynomialCalculate the roots r of the polynomial p. | |
| cvec | itpp::roots (const cvec &p) |
Calculate the roots of the polynomialCalculate the roots r of the polynomial p. | |
| vec | itpp::polyval (const vec &p, const vec &x) |
Evaluate polynomialEvaluate the polynomial p (of length 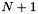 at the points at the points x The output is given by
. | |
| cvec | itpp::polyval (const vec &p, const cvec &x) |
Evaluate polynomialEvaluate the polynomial p (of length 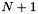 at the points at the points x The output is given by
. | |
| cvec | itpp::polyval (const cvec &p, const vec &x) |
Evaluate polynomialEvaluate the polynomial p (of length 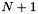 at the points at the points x The output is given by
. | |
| cvec | itpp::polyval (const cvec &p, const cvec &x) |
Evaluate polynomialEvaluate the polynomial p (of length 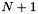 at the points at the points x The output is given by
. | |
| ITPP_EXPORT double itpp::cheb | ( | int | n, |
| double | x | ||
| ) |
Chebyshev polynomial of the first kindChebyshev polynomials of the first kind can be defined as follows:
![\[ T(x) = \left\{ \begin{array}{ll} \cos(n\arccos(x)),& |x| \leq 0 \\ \cosh(n\mathrm{arccosh}(x)),& x > 1 \\ (-1)^n \cosh(n\mathrm{arccosh}(-x)),& x < -1 \end{array} \right. \]](form_258.png)
.
| n | order of the Chebyshev polynomial |
| x | value at which the Chebyshev polynomial is to be evaluated |
Definition at line 195 of file poly.cpp.
References itpp::acos(), itpp::acosh(), itpp::cos(), itpp::cosh(), itpp::is_even(), and it_assert.
Referenced by itpp::cheb(), and itpp::chebwin().
| ITPP_EXPORT vec itpp::cheb | ( | int | n, |
| const vec & | x | ||
| ) |
Chebyshev polynomial of the first kindChebyshev polynomials of the first kind can be defined as follows:
![\[ T(x) = \left\{ \begin{array}{ll} \cos(n\arccos(x)),& |x| \leq 0 \\ \cosh(n\mathrm{arccosh}(x)),& x > 1 \\ (-1)^n \cosh(n\mathrm{arccosh}(-x)),& x < -1 \end{array} \right. \]](form_258.png)
.
| n | order of the Chebyshev polynomial |
| x | vector of values at which the Chebyshev polynomial is to be evaluated |
x Definition at line 209 of file poly.cpp.
References itpp::cheb(), and it_assert_debug.
| ITPP_EXPORT mat itpp::cheb | ( | int | n, |
| const mat & | x | ||
| ) |
Chebyshev polynomial of the first kindChebyshev polynomials of the first kind can be defined as follows:
![\[ T(x) = \left\{ \begin{array}{ll} \cos(n\arccos(x)),& |x| \leq 0 \\ \cosh(n\mathrm{arccosh}(x)),& x > 1 \\ (-1)^n \cosh(n\mathrm{arccosh}(-x)),& x < -1 \end{array} \right. \]](form_258.png)
.
| n | order of the Chebyshev polynomial |
| x | matrix of values at which the Chebyshev polynomial is to be evaluated |
x.Definition at line 220 of file poly.cpp.
References itpp::cheb(), and it_assert_debug.
Generated on Sat May 25 2013 16:32:27 for IT++ by Doxygen 1.8.2