
Functions | |
| double | itpp::besselj (int nu, double x) |
| Bessel function of first kind of order nu for nu integer. | |
| vec | itpp::besselj (int nu, const vec &x) |
| Bessel function of first kind of order nu for nu integer. | |
| double | itpp::besselj (double nu, double x) |
| Bessel function of first kind of order nu. nu is real. | |
| vec | itpp::besselj (double nu, const vec &x) |
| Bessel function of first kind of order nu. nu is real. | |
| double | itpp::bessely (int nu, double x) |
| Bessel function of second kind of order nu. nu is integer. | |
| vec | itpp::bessely (int nu, const vec &x) |
| Bessel function of second kind of order nu. nu is integer. | |
| double | itpp::bessely (double nu, double x) |
| Bessel function of second kind of order nu. nu is real. | |
| vec | itpp::bessely (double nu, const vec &x) |
| Bessel function of second kind of order nu. nu is real. | |
| double | itpp::besseli (double nu, double x) |
| Modified Bessel function of first kind of order nu. nu is double. x is double. | |
| vec | itpp::besseli (double nu, const vec &x) |
| Modified Bessel function of first kind of order nu. nu is double. x is double. | |
| double | itpp::besselk (int nu, double x) |
| Modified Bessel function of second kind of order nu. nu is double. x is double. | |
| vec | itpp::besselk (int nu, const vec &x) |
| Modified Bessel function of second kind of order nu. nu is double. x is double. | |
end of math group
| ITPP_EXPORT double itpp::besselj | ( | int | nu, |
| double | x | ||
| ) |
Bessel function of first kind of order nu for nu integer.
The bessel function of first kind is defined as:
![\[ J_{\nu}(x) = \sum_{k=0}^{\infty} \frac{ (-1)^{k} }{k! \Gamma(\nu+k+1) } \left(\frac{x}{2}\right)^{\nu+2k} \]](form_0.png)
where 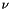 is the order and
is the order and  .
.
Definition at line 44 of file bessel.cpp.
Referenced by itpp::FIR_Fading_Generator::Jakes_filter().
| ITPP_EXPORT double itpp::bessely | ( | int | nu, |
| double | x | ||
| ) |
Bessel function of second kind of order nu. nu is integer.
The Bessel function of second kind is defined as:
![\[ Y_{\nu}(x) = \frac{J_{\nu}(x) \cos(\nu\pi) - J_{-\nu}(x)}{\sin(\nu\pi)} \]](form_3.png)
where 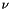 is the order and
is the order and  .
.
Definition at line 68 of file bessel.cpp.
| ITPP_EXPORT double itpp::besseli | ( | double | nu, |
| double | x | ||
| ) |
Modified Bessel function of first kind of order nu. nu is double. x is double.
The Modified Bessel function of first kind is defined as:
![\[ I_{\nu}(x) = i^{-\nu} J_{\nu}(ix) \]](form_4.png)
where 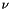 is the order and
is the order and  .
.
Definition at line 91 of file bessel.cpp.
| ITPP_EXPORT double itpp::besselk | ( | int | nu, |
| double | x | ||
| ) |
Modified Bessel function of second kind of order nu. nu is double. x is double.
The Modified Bessel function of second kind is defined as:
![\[ K_{\nu}(x) = \frac{\pi}{2} i^{\nu+1} [J_{\nu}(ix) + i Y_{\nu}(ix)] \]](form_5.png)
where 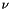 is the order and
is the order and  .
.
Definition at line 103 of file bessel.cpp.
Generated on Sat Jul 6 2013 10:54:28 for IT++ by Doxygen 1.8.2