
M-ary QAM modulator with square lattice. More...
#include <itpp/comm/modulator.h>
Public Member Functions | |
| QAM () | |
| Default Constructor. | |
| QAM (int M) | |
| Class Constructor. | |
| virtual | ~QAM () |
| Destructor. | |
| void | set_M (int M) |
| Change the size of the signal constellation. | |
| void | demodulate_bits (const cvec &signal, bvec &bits) const |
| Hard demodulation of bits. | |
| bvec | demodulate_bits (const cvec &signal) const |
| Hard demodulation of bits. | |
| virtual void | set (const Vec< std::complex< double > > &symbols, const ivec &bits2symbols) |
| Set the constellation to use in the modulator. | |
| virtual int | bits_per_symbol () const |
| Returns number of bits per symbol. | |
| virtual int | get_k () const |
| Returns number of bits per symbol. | |
| virtual int | get_M () const |
| Returns number of modulation symbols. | |
|
virtual Vec< std::complex < double > > | get_symbols () const |
| Get the symbol values used in the modulator. | |
| virtual ivec | get_bits2symbols () const |
| Get the bitmap, which maps input bits into symbols. | |
| virtual void | modulate (const ivec &symbolnumbers, Vec< std::complex< double > > &output) const |
| Modulation of symbols. | |
|
virtual Vec< std::complex < double > > | modulate (const ivec &symbolnumbers) const |
| Modulation of symbols. | |
| virtual void | demodulate (const Vec< std::complex< double > > &signal, ivec &output) const |
| Demodulation of symbols. | |
| virtual ivec | demodulate (const Vec< std::complex< double > > &signal) const |
| Demodulation of symbols. | |
| virtual void | modulate_bits (const bvec &bits, Vec< std::complex< double > > &output) const |
| Modulation of bits. | |
|
virtual Vec< std::complex < double > > | modulate_bits (const bvec &bits) const |
| Modulation of bits. | |
| virtual void | demodulate_bits (const Vec< std::complex< double > > &signal, bvec &bits) const |
| Hard demodulation of bits. | |
| virtual bvec | demodulate_bits (const Vec< std::complex< double > > &signal) const |
| Hard demodulation of bits. | |
| virtual void | demodulate_soft_bits (const Vec< std::complex< double > > &rx_symbols, double N0, vec &soft_bits, Soft_Method method=LOGMAP) const |
| Soft demodulator for AWGN channels. | |
| virtual vec | demodulate_soft_bits (const Vec< std::complex< double > > &rx_symbols, double N0, Soft_Method method=LOGMAP) const |
| Soft demodulator for AWGN channels. | |
| virtual void | demodulate_soft_bits (const Vec< std::complex< double > > &rx_symbols, const Vec< std::complex< double > > &channel, double N0, vec &soft_bits, Soft_Method method=LOGMAP) const |
| Soft demodulator for fading channels. | |
| virtual vec | demodulate_soft_bits (const Vec< std::complex< double > > &rx_symbols, const Vec< std::complex< double > > &channel, double N0, Soft_Method method=LOGMAP) const |
| Soft demodulator for fading channels. | |
Protected Member Functions | |
| void | calculate_softbit_matrices () |
| This function calculates the soft bit mapping matrices S0 and S1. | |
Protected Attributes | |
| int | L |
| The square-root of M. | |
| double | scaling_factor |
| Scaling factor of square QAM constellation (sqrt((M-1)*2/3)) | |
| bool | setup_done |
| Setup indicator. | |
| int | k |
| Number of bits per modulation symbol. | |
| int | M |
| Number of modulation symbols. | |
| bmat | bitmap |
| Bit to symbol mapping table (size: M x k) | |
| ivec | bits2symbols |
| Bit to symbol mapping in decimal form (size: M) | |
| Vec< std::complex< double > > | symbols |
| Corresponding modulation symbols (size: M) | |
| imat | S0 |
| Matrix where row k contains the constellation points with '0' in bit position k. | |
| imat | S1 |
| Matrix where row k contains the constellation points with '1' in bit position k. | |
Related Functions | |
(Note that these are not member functions.) | |
| typedef Modulator< double > | Modulator_1D |
| Definition of 1D Modulator (with real symbols) | |
|
typedef Modulator < std::complex< double > > | Modulator_2D |
| Definition of 2D Modulator (with complex symbols) | |
M-ary QAM modulator with square lattice.
The size of the QAM constellation is 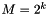 , where
, where 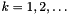 . Symbol values in each dimension are:
. Symbol values in each dimension are: 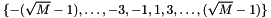 . The bitmap is Gray encoded. Symbols are normalized so that the average energy is 1. That is, normalized with
. The bitmap is Gray encoded. Symbols are normalized so that the average energy is 1. That is, normalized with 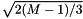 .
.
Beside hard demapping, this class can also perform soft demodulation, calculating the log-MAP estimate of the individual bits. To use it properly the received symbols should be equal to:
![\[r_k = c_k s_k + n_k,\]](form_132.png)
where 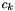 is the real or complex channel gain,
is the real or complex channel gain, 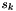 is the transmitted constellation symbol, and
is the transmitted constellation symbol, and 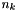 is the AWGN of the channel (with variance
is the AWGN of the channel (with variance 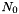 ).
).
It is also assumed that the channel estimates are perfect when calculating the soft bits.
Definition at line 586 of file modulator.h.
|
inlinevirtualinherited |
Get the bitmap, which maps input bits into symbols.
The mapping is done as follows. An input bit sequence in decimal notation is used for indexing the bits2symbols table. The indexing result denotes the symbol to be used from the symbols table, e.g.:
Definition at line 117 of file modulator.h.
References itpp::Modulator< T >::bits2symbols.
|
virtualinherited |
Soft demodulator for AWGN channels.
This function calculates the log-likelihood ratio (LLR) of the received signal from AWGN channels. Depending on the soft demodulation method chosen, either full log-MAP calculation is performed (default method), according to the following equation:
![\[\log \left( \frac{P(b_i=0|r)}{P(b_i=1|r)} \right) = \log \left( \frac{\sum_{s_i \in S_0} \exp \left( -\frac{|r_k - s_i|^2}{N_0} \right)} {\sum_{s_i \in S_1} \exp \left( -\frac{|r_k - s_i|^2}{N_0} \right)} \right) \]](form_149.png)
or approximate, but faster calculation is performed.
The approximate method finds for each bit the closest constellation points that have zero and one in the corresponding position. Let 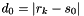 denote the distance to the closest zero point and
denote the distance to the closest zero point and 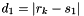 denote the distance to the closest one point for the corresponding bit respectively. The approximate algorithm then computes
denote the distance to the closest one point for the corresponding bit respectively. The approximate algorithm then computes
![\[\frac{d_1^2 - d_0^2}{N_0}\]](form_152.png)
This function can be used on channels where the channel gain  .
.
When this function is to be used together with MAP-based turbo decoding algorithms then the channel reliability factor 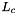 of the turbo decoder shall be set to 1. The output from this function can also be used by a Viterbi decoder using an AWGN based metric calculation function.
of the turbo decoder shall be set to 1. The output from this function can also be used by a Viterbi decoder using an AWGN based metric calculation function.
| rx_symbols | The received noisy constellation symbols |
| N0 | The spectral density of the AWGN noise |
| soft_bits | The soft bits calculated using the expression above |
| method | The method used for demodulation (LOGMAP or APPROX) |
Modulator_ND) instead, which is based on the QLLR (quantized) arithmetic and therefore is faster. Please note, however, that mixed use of Modulator_1D/Modulator_2D and Modulator_ND is not advised.
|
virtualinherited |
Soft demodulator for fading channels.
This function calculates the log-likelihood ratio (LLR) of the received signal from fading channels. Depending on the soft demodulation method chosen, either full log-MAP calculation is performed (default method), according to the following equation:
![\[\log \left( \frac{P(b_i=0|r)}{P(b_i=1|r)} \right) = \log \left( \frac{\sum_{s_i \in S_0} \exp \left( -\frac{|r_k - c_k s_i|^2}{N_0} \right)} {\sum_{s_i \in S_1} \exp \left( -\frac{|r_k - c_k s_i|^2}{N_0} \right)} \right) \]](form_155.png)
or approximate, but faster calculation is performed.
The approximate method finds for each bit the closest constellation points that have zero and one in the corresponding position. Let  denote the distance to the closest zero point and
denote the distance to the closest zero point and 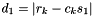 denote the distance to the closest one point for the corresponding bit respectively. The approximate algorithm then computes
denote the distance to the closest one point for the corresponding bit respectively. The approximate algorithm then computes
![\[\frac{d_1^2 - d_0^2}{N_0}\]](form_152.png)
When this function is to be used together with MAP-based turbo decoding algorithms then the channel reliability factor  of the turbo decoder shall be set to 1. The output from this function can also be used by a Viterbi decoder using an AWGN based metric calculation function.
of the turbo decoder shall be set to 1. The output from this function can also be used by a Viterbi decoder using an AWGN based metric calculation function.
| rx_symbols | The received noisy constellation symbols  |
| channel | The channel values  |
| N0 | The spectral density of the AWGN noise |
| soft_bits | The soft bits calculated using the expression above |
| method | The method used for demodulation (LOGMAP or APPROX) |
Modulator_1D/Modulator_2D and Modulator_ND is not advised. Generated on Sat Jul 6 2013 10:54:32 for IT++ by Doxygen 1.8.2