Windowing functions. More...
Functions | |
| vec | itpp::hamming (int size) |
| Hamming window. | |
| vec | itpp::hanning (int n) |
| Hanning window. | |
| vec | itpp::hann (int n) |
| Hanning window compatible with matlab. | |
| vec | itpp::blackman (int n) |
| Blackman window. | |
| vec | itpp::triang (int n) |
| Triangular window. | |
| vec | itpp::sqrt_win (int n) |
| Square root window. | |
| vec | itpp::chebwin (int n, double at) |
| Dolph-Chebyshev window. | |
Windowing functions.
| ITPP_EXPORT vec itpp::hamming | ( | int | size | ) |
Hamming window.
The n size Hamming window is a vector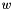 
where the 
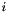th component is
![\[ w_i = 0.54 - 0.46 \cos(2\pi i/(n-1)) \]](form_271.png)
Definition at line 43 of file window.cpp.
References itpp::cos(), and itpp::pi.
Referenced by itpp::fir1(), and itpp::FIR_Fading_Generator::Jakes_filter().
| ITPP_EXPORT vec itpp::hanning | ( | int | n | ) |
Hanning window.
The n size Hanning window is a vector 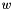where the 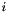th component is
![\[ w_i = 0.5(1 - \cos(2\pi (i+1)/(n+1)) \]](form_272.png)
Observe that this function is not the same as the hann() function which is defined as in matlab.
Definition at line 56 of file window.cpp.
References itpp::cos(), and itpp::pi.
Referenced by itpp::spectrum().
| ITPP_EXPORT vec itpp::hann | ( | int | n | ) |
Hanning window compatible with matlab.
The n size Hanning window is a vector 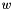where the 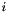th component is
![\[ w_i = 0.5(1 - \cos(2\pi i/(n-1)) \]](form_273.png)
Definition at line 67 of file window.cpp.
References itpp::cos(), and itpp::pi.
| ITPP_EXPORT vec itpp::blackman | ( | int | n | ) |
Blackman window.
The n size Blackman window is a vector 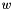where the 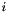th component is
![\[ w_i = 0.42 - 0.5\cos(2\pi i/(n-1)) + 0.08\cos(4\pi i/(n-1)) \]](form_274.png)
Definition at line 77 of file window.cpp.
References itpp::cos(), and itpp::pi.
| ITPP_EXPORT vec itpp::triang | ( | int | n | ) |
Triangular window.
The n size triangle window is a vector 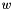where the 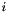th component is
![\[ w_i = w_{n-i-1} = \frac{2(i+1)}{n+1} \]](form_275.png)
for n odd and for n even
![\[ w_i = w_{n-i-1} = \frac{2i+1}{n} \]](form_276.png)
Definition at line 87 of file window.cpp.
| ITPP_EXPORT vec itpp::sqrt_win | ( | int | n | ) |
Square root window.
The square-root of the Triangle window. sqrt_win(n) = sqrt(triang(n))
Definition at line 103 of file window.cpp.
References itpp::sqrt().
| ITPP_EXPORT vec itpp::chebwin | ( | int | n, |
| double | at | ||
| ) |
Dolph-Chebyshev window.
The length n Dolph-Chebyshev window is a vector 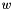whose 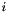th transform component is given by
![\[ W[k] = \frac{T_M\left(\beta \cos\left(\frac{\pi k}{M}\right) \right)}{T_M(\beta)},k = 0, 1, 2, \ldots, M - 1 \]](form_277.png)
where T_n(x) is the order n Chebyshev polynomial of the first kind.
| n | length of the Doplh-Chebyshev window |
| at | attenutation of side lobe (in dB) |
n Doplh-Chebyshev windowDefinition at line 119 of file window.cpp.
References itpp::acosh(), itpp::cheb(), itpp::concat(), itpp::cos(), itpp::cosh(), itpp::elem_mult(), itpp::ifft_real(), itpp::is_even(), it_assert, itpp::linspace(), itpp::pi, itpp::pow10(), itpp::reverse(), itpp::Vec< Num_T >::right(), itpp::sin(), and itpp::to_cvec().
Generated on Sat Jul 6 2013 10:54:29 for IT++ by Doxygen 1.8.2