Classes
class	itpp::Filter< T1, T2, T3 >
	Virtual Filter Base Class.The class is templated as follows: More...

class	itpp::MA_Filter< T1, T2, T3 >
	Moving Average Filter Base Class.This class implements a moving average (MA) filter according to $y(n) = b(0)x(n) + b(1)x(n-1) + ... + b(N)*x(n-N)$ where b is the filter coefficients, x is the input and y is the output. More...

class	itpp::AR_Filter< T1, T2, T3 >
	Autoregressive (AR) Filter Base Class.This class implements a autoregressive (AR) filter according to $a(0)y(n) = x(n) - a(1)y(n-1) - ... - a(N)*y(n-N)$ where a is the filter coefficients, x is the input and y is the output. More...

class	itpp::ARMA_Filter< T1, T2, T3 >
	Autoregressive Moving Average (ARMA) Filter Base Class.This class implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ . More...

class	itpp::Freq_Filt< Num_T >
	Freq_Filt Frequency domain filtering using the overlap-add techniqueThe Freq_Filt class implements an FFT based filter using the overlap-add technique. The data is filtered by first transforming the input sequence into the frequency domain with an efficient FFT implementation (i.e. FFTW) and then multiplied with a Fourier transformed version of the impulse response. The resulting data is then inversed Fourier transformed to return a filtered time domain signal. More...

Functions
vec	itpp::fir1 (int N, double cutoff)
	Design a Nth order FIR filter with cut-off frequency `cutoff` using the window method.

void	itpp::filter_design_autocorrelation (const int N, const vec &f, const vec &m, vec &R)
	Calculate autocorrelation from the specified frequency-response (suitable for filter design)

void	itpp::modified_yule_walker (const int m, const int n, const int N, const vec &R, vec &a)
	Estimation of AR-part in an ARMA model given the autocorrelation.

void	itpp::arma_estimator (const int m, const int n, const vec &R, vec &b, vec &a)
	Estimation of ARMA model given the autocorrelation.

void	itpp::yulewalk (const int N, const vec &f, const vec &m, vec &b, vec &a)
	ARMA filter design using a least-squares fit to the specified frequency-response.

vec	itpp::filter (const vec &b, const vec &a, const vec &input)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const vec &b, const vec &a, const cvec &input)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const cvec &b, const cvec &a, const cvec &input)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const cvec &b, const cvec &a, const vec &input)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

vec	itpp::filter (const vec &b, const int one, const vec &input)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const vec &b, const int one, const cvec &input)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const cvec &b, const int one, const cvec &input)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const cvec &b, const int one, const vec &input)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

vec	itpp::filter (const int one, const vec &a, const vec &input)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const int one, const vec &a, const cvec &input)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const int one, const cvec &a, const cvec &input)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const int one, const cvec &a, const vec &input)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

vec	itpp::filter (const vec &b, const vec &a, const vec &input, const vec &state_in, vec &state_out)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const vec &b, const vec &a, const cvec &input, const cvec &state_in, cvec &state_out)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const cvec &b, const cvec &a, const cvec &input, const cvec &state_in, cvec &state_out)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const cvec &b, const cvec &a, const vec &input, const cvec &state_in, cvec &state_out)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

vec	itpp::filter (const vec &b, const int one, const vec &input, const vec &state_in, vec &state_out)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const vec &b, const int one, const cvec &input, const cvec &state_in, cvec &state_out)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const cvec &b, const int one, const cvec &input, const cvec &state_in, cvec &state_out)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const cvec &b, const int one, const vec &input, const cvec &state_in, cvec &state_out)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

vec	itpp::filter (const int one, const vec &a, const vec &input, const vec &state_in, vec &state_out)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const int one, const vec &a, const cvec &input, const cvec &state_in, cvec &state_out)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const int one, const cvec &a, const cvec &input, const cvec &state_in, cvec &state_out)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

cvec	itpp::filter (const int one, const cvec &a, const vec &input, const cvec &state_in, cvec &state_out)
	ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to $a(0)y(n) = b(0)x(n) + b(1)x(n-1) + \ldots + b(N_b)x(n-N_b) - a(1)y(n-1) - \ldots - a(N_a)y(n-N_a)$ .

void	itpp::polystab (const vec &a, vec &out)
	Polynomial Stabilization.

void	itpp::polystab (const cvec &a, cvec &out)
	Polynomial Stabilization.

vec	itpp::polystab (const vec &a)
	Polynomial Stabilization.

cvec	itpp::polystab (const cvec &a)
	Polynomial Stabilization.

void	itpp::freqz (const cvec &b, const cvec &a, const int N, cvec &h, vec &w)
	Frequency response of filter.

cvec	itpp::freqz (const cvec &b, const cvec &a, const int N)
	Frequency response of filter.

cvec	itpp::freqz (const cvec &b, const cvec &a, const vec &w)
	Frequency response of filter.

void	itpp::freqz (const vec &b, const vec &a, const int N, cvec &h, vec &w)
	Frequency response of filter.

cvec	itpp::freqz (const vec &b, const vec &a, const int N)
	Frequency response of filter.

cvec	itpp::freqz (const vec &b, const vec &a, const vec &w)
	Frequency response of filter.

Detailed Description

Function Documentation

ITPP_EXPORT vec itpp::filter	(	const vec &	b,
		const vec &	a,
		const vec &	input
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 39 of file filter.cpp.

Referenced by itpp::arma_estimator(), and itpp::Filter< T1, T2, T3 >::operator()().

ITPP_EXPORT void itpp::polystab	(	const vec &	a,
		vec &	out
	)

Polynomial Stabilization.

Author: Tony Ottosson

Stabilizes the polynomial transfer function by replacing all roots outside the unit cirlce with their reflection inside the unit circle.

Definition at line 45 of file filter_design.cpp.

References itpp::abs(), itpp::conj(), itpp::poly(), itpp::real(), and itpp::roots().

Referenced by itpp::modified_yule_walker(), and itpp::polystab().

ITPP_EXPORT void itpp::freqz	(	const cvec &	b,
		const cvec &	a,
		const int	N,
		cvec &	h,
		vec &	w
	)

Frequency response of filter.

Author: Tony Ottosson

Calculates the N-point frequency response of the supplied digital filter over the frequencies w. If w is not given the response is evaluated over the range 0 to 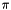$\pi$ with N values. The default value of N is 512.

If w is supplied polyval() is used. Otherwise the calculation is based on the fft.

Definition at line 71 of file filter_design.cpp.

References itpp::elem_div(), itpp::fft(), itpp::linspace(), and itpp::pi.

Referenced by itpp::freqz().

ITPP_EXPORT void itpp::filter_design_autocorrelation	(	const int	N,
		const vec &	f,
		const vec &	m,
		vec &	R
	)

Calculate autocorrelation from the specified frequency-response (suitable for filter design)

Author: Tony Ottosson

Calculates the autocorrelation function of size N corresponding to the specified frequency response. Useful as a first step in designing filters.

The vectors f and m is the frequency response. The frequencies should be between 0 and 1.0 (equal to half the sample rate) in increasing order. Both 0.0 and 1.0 must be included. The frequency response is upsampled to 512 points and the autocorrelation is ifft of the power magnitude response of the upsampled frequency response.

Definition at line 153 of file filter_design.cpp.

References itpp::concat(), itpp::floor_i(), itpp::ifft_real(), it_assert, itpp::reverse(), itpp::sqr(), and itpp::to_cvec().

Referenced by itpp::yulewalk().

ITPP_EXPORT void itpp::modified_yule_walker	(	const int	m,
		const int	n,
		const int	N,
		const vec &	R,
		vec &	a
	)

Estimation of AR-part in an ARMA model given the autocorrelation.

Author: Tony Ottosson

Estimates the AR-part of an ARMA model from the given autocorrelation. The AR part is of order n. The overdetermined modified Yule-Walker equations are used.

If 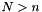$N>n$ then the system is overdetermined and a least squares solution is used. As a rule of thumb use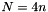 $N = 4 n$

The parameter m is the order of the MA-part such that 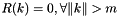$R(k) = 0, \forall \|k\| > m$ .

The supplied autocorrelation should at least be of size N.

References: Stoica and Moses, Introduction to spectral analysis, Prentice Hall, 1997.

Definition at line 197 of file filter_design.cpp.

References itpp::abs(), itpp::backslash(), itpp::concat(), it_assert, itpp::polystab(), itpp::reverse(), and itpp::toeplitz().

Referenced by itpp::arma_estimator().

ITPP_EXPORT void itpp::arma_estimator	(	const int	m,
		const int	n,
		const vec &	R,
		vec &	b,
		vec &	a
	)

Estimation of ARMA model given the autocorrelation.

Author: Tony Ottosson

Estimates an ARMA model from the given autocorrelation. The AR part is of order n and the MA part is of order m.

The AR part (the denominator) is calcuated using the modified Yule-Walker equations. The the MA part (the nominator) is calculated by calculating the inverse magnitude spectrum using FFTs of size 512 which is an AR-system. This AR-system is then solved using the Levinson-Durbin algorithm.

The supplied autocorrelation is windowed using a Hamming window of size 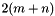$2(m+n)$ and hence should at least be of that size.

References: [1] Stoica and Moses, Introduction to spectral analysis, Prentice Hall, 1997. [2] B. Friedlander and B. Porat, The modified Yule-Walker method of ARMA spectral estimation, IEEE Trans. Aerospace and Electronic Systems, Vol. AES-20, No. 2, pp. 158–173, March 1984.

Definition at line 228 of file filter_design.cpp.

References itpp::backslash(), itpp::concat(), itpp::cos(), itpp::elem_div(), itpp::elem_mult(), itpp::exp(), itpp::fft(), itpp::fft_real(), itpp::filter(), itpp::ifft(), it_assert, itpp::linspace(), itpp::log(), itpp::modified_yule_walker(), itpp::pi, itpp::real(), itpp::to_cmat(), itpp::to_cvec(), itpp::toeplitz(), itpp::zeros(), and itpp::zeros_c().

Referenced by itpp::yulewalk().

ITPP_EXPORT void itpp::yulewalk	(	const int	N,
		const vec &	f,
		const vec &	m,
		vec &	b,
		vec &	a
	)

ARMA filter design using a least-squares fit to the specified frequency-response.

Author: Tony Ottosson

The arma_estimator() function is used to calculate the a and b coefficients.

The vectors f and m is the frequency response. The frequencies should be between 0 and 1.0 (equal to half the sample rate) in increasing order. Both 0.0 and 1.0 must be included. The filter_design_autocorrelation() fucnction is used to interpolate the frequency response and calculate the corresponding autocorrelation.

Observe: this function will not always give exactly the same result as the matlab yulewalk function.

Definition at line 269 of file filter_design.cpp.

References itpp::arma_estimator(), itpp::filter_design_autocorrelation(), and it_assert.

ITPP_EXPORT cvec itpp::filter	(	const vec &	b,
		const vec &	a,
		const cvec &	input
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 45 of file filter.cpp.

ITPP_EXPORT cvec itpp::filter	(	const cvec &	b,
		const cvec &	a,
		const cvec &	input
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 51 of file filter.cpp.

ITPP_EXPORT cvec itpp::filter	(	const cvec &	b,
		const cvec &	a,
		const vec &	input
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 57 of file filter.cpp.

ITPP_EXPORT vec itpp::filter	(	const vec &	b,
		const int	one,
		const vec &	input
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 64 of file filter.cpp.

References it_assert.

ITPP_EXPORT cvec itpp::filter	(	const vec &	b,
		const int	one,
		const cvec &	input
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 71 of file filter.cpp.

References it_assert.

ITPP_EXPORT cvec itpp::filter	(	const cvec &	b,
		const int	one,
		const cvec &	input
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 78 of file filter.cpp.

References it_assert.

ITPP_EXPORT cvec itpp::filter	(	const cvec &	b,
		const int	one,
		const vec &	input
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 85 of file filter.cpp.

References it_assert.

ITPP_EXPORT vec itpp::filter	(	const int	one,
		const vec &	a,
		const vec &	input
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 93 of file filter.cpp.

References it_assert.

ITPP_EXPORT cvec itpp::filter	(	const int	one,
		const vec &	a,
		const cvec &	input
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 100 of file filter.cpp.

References it_assert.

ITPP_EXPORT cvec itpp::filter	(	const int	one,
		const cvec &	a,
		const cvec &	input
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 107 of file filter.cpp.

References it_assert.

ITPP_EXPORT cvec itpp::filter	(	const int	one,
		const cvec &	a,
		const vec &	input
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 114 of file filter.cpp.

References it_assert.

ITPP_EXPORT vec itpp::filter	(	const vec &	b,
		const vec &	a,
		const vec &	input,
		const vec &	state_in,
		vec &	state_out
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 125 of file filter.cpp.

References itpp::ARMA_Filter< T1, T2, T3 >::get_state(), and itpp::ARMA_Filter< T1, T2, T3 >::set_state().

ITPP_EXPORT cvec itpp::filter	(	const vec &	b,
		const vec &	a,
		const cvec &	input,
		const cvec &	state_in,
		cvec &	state_out
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 134 of file filter.cpp.

References itpp::ARMA_Filter< T1, T2, T3 >::get_state(), and itpp::ARMA_Filter< T1, T2, T3 >::set_state().

ITPP_EXPORT cvec itpp::filter	(	const cvec &	b,
		const cvec &	a,
		const cvec &	input,
		const cvec &	state_in,
		cvec &	state_out
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 143 of file filter.cpp.

References itpp::ARMA_Filter< T1, T2, T3 >::get_state(), and itpp::ARMA_Filter< T1, T2, T3 >::set_state().

ITPP_EXPORT cvec itpp::filter	(	const cvec &	b,
		const cvec &	a,
		const vec &	input,
		const cvec &	state_in,
		cvec &	state_out
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 152 of file filter.cpp.

References itpp::ARMA_Filter< T1, T2, T3 >::get_state(), and itpp::ARMA_Filter< T1, T2, T3 >::set_state().

ITPP_EXPORT vec itpp::filter	(	const vec &	b,
		const int	one,
		const vec &	input,
		const vec &	state_in,
		vec &	state_out
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 162 of file filter.cpp.

References itpp::MA_Filter< T1, T2, T3 >::get_state(), it_assert, and itpp::MA_Filter< T1, T2, T3 >::set_state().

ITPP_EXPORT cvec itpp::filter	(	const vec &	b,
		const int	one,
		const cvec &	input,
		const cvec &	state_in,
		cvec &	state_out
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 172 of file filter.cpp.

References itpp::MA_Filter< T1, T2, T3 >::get_state(), it_assert, and itpp::MA_Filter< T1, T2, T3 >::set_state().

ITPP_EXPORT cvec itpp::filter	(	const cvec &	b,
		const int	one,
		const cvec &	input,
		const cvec &	state_in,
		cvec &	state_out
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 182 of file filter.cpp.

References itpp::MA_Filter< T1, T2, T3 >::get_state(), it_assert, and itpp::MA_Filter< T1, T2, T3 >::set_state().

ITPP_EXPORT cvec itpp::filter	(	const cvec &	b,
		const int	one,
		const vec &	input,
		const cvec &	state_in,
		cvec &	state_out
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 192 of file filter.cpp.

References itpp::MA_Filter< T1, T2, T3 >::get_state(), it_assert, and itpp::MA_Filter< T1, T2, T3 >::set_state().

ITPP_EXPORT vec itpp::filter	(	const int	one,
		const vec &	a,
		const vec &	input,
		const vec &	state_in,
		vec &	state_out
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 203 of file filter.cpp.

References itpp::AR_Filter< T1, T2, T3 >::get_state(), it_assert, and itpp::AR_Filter< T1, T2, T3 >::set_state().

ITPP_EXPORT cvec itpp::filter	(	const int	one,
		const vec &	a,
		const cvec &	input,
		const cvec &	state_in,
		cvec &	state_out
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 213 of file filter.cpp.

References itpp::AR_Filter< T1, T2, T3 >::get_state(), it_assert, and itpp::AR_Filter< T1, T2, T3 >::set_state().

ITPP_EXPORT cvec itpp::filter	(	const int	one,
		const cvec &	a,
		const cvec &	input,
		const cvec &	state_in,
		cvec &	state_out
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 223 of file filter.cpp.

References itpp::AR_Filter< T1, T2, T3 >::get_state(), it_assert, and itpp::AR_Filter< T1, T2, T3 >::set_state().

ITPP_EXPORT cvec itpp::filter	(	const int	one,
		const cvec &	a,
		const vec &	input,
		const cvec &	state_in,
		cvec &	state_out
	)

ARMA filter functionThese functions implements a autoregressive moving average (ARMA) filter according to

$a(0)*y(n) = b(0)*x(n) + b(1)*x(n-1) + \ldots + b(N_b)*x(n-N_b) - a(1)*y(n-1) - \ldots - a(N_a)*y(n-N_a)$

.

where a and b are the filter coefficients, x is the input and y is the output.

Setting a=1 gives a MA filter and b=1 gives a AR filter. The length of the output vector equals the length of the input vector. The state vectors state_in and state_out is of length $max(N_a, n_b) - 1$ .

If no start state state_in is given it is set to zero.

Definition at line 233 of file filter.cpp.

References itpp::AR_Filter< T1, T2, T3 >::get_state(), it_assert, and itpp::AR_Filter< T1, T2, T3 >::set_state().

ITPP_EXPORT void itpp::polystab	(	const cvec &	a,
		cvec &	out
	)

Polynomial Stabilization.

Author: Tony Ottosson

Stabilizes the polynomial transfer function by replacing all roots outside the unit cirlce with their reflection inside the unit circle.

Definition at line 57 of file filter_design.cpp.

References itpp::abs(), itpp::conj(), itpp::poly(), and itpp::roots().

ITPP_EXPORT cvec itpp::freqz	(	const cvec &	b,
		const cvec &	a,
		const int	N
	)

Frequency response of filter.

Author: Tony Ottosson

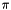Calculates the N-point frequency response of the supplied digital filter over the frequencies w. If w is not given the response is evaluated over the range 0 to $\pi$ with N values. The default value of N is 512.

If w is supplied polyval() is used. Otherwise the calculation is based on the fft.

Definition at line 85 of file filter_design.cpp.

References itpp::freqz().

ITPP_EXPORT cvec itpp::freqz	(	const cvec &	b,
		const cvec &	a,
		const vec &	w
	)

Frequency response of filter.

Author: Tony Ottosson

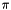Calculates the N-point frequency response of the supplied digital filter over the frequencies w. If w is not given the response is evaluated over the range 0 to $\pi$ with N values. The default value of N is 512.

If w is supplied polyval() is used. Otherwise the calculation is based on the fft.

Definition at line 96 of file filter_design.cpp.

References itpp::cos(), itpp::elem_div(), itpp::max(), itpp::polyval(), itpp::sin(), itpp::to_cvec(), and itpp::zero_pad().

ITPP_EXPORT void itpp::freqz	(	const vec &	b,
		const vec &	a,
		const int	N,
		cvec &	h,
		vec &	w
	)

Frequency response of filter.

Author: Tony Ottosson

Calculates the N-point frequency response of the supplied digital filter over the frequencies w. If w is not given the response is evaluated over the range 0 to 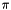$\pi$ with N values. The default value of N is 512.

If w is supplied polyval() is used. Otherwise the calculation is based on the fft.

Definition at line 111 of file filter_design.cpp.

References itpp::elem_div(), itpp::fft_real(), itpp::linspace(), and itpp::pi.

ITPP_EXPORT cvec itpp::freqz	(	const vec &	b,
		const vec &	a,
		const int	N
	)

Frequency response of filter.

Author: Tony Ottosson

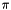Calculates the N-point frequency response of the supplied digital filter over the frequencies w. If w is not given the response is evaluated over the range 0 to $\pi$ with N values. The default value of N is 512.

If w is supplied polyval() is used. Otherwise the calculation is based on the fft.

Definition at line 125 of file filter_design.cpp.

References itpp::freqz().

ITPP_EXPORT cvec itpp::freqz	(	const vec &	b,
		const vec &	a,
		const vec &	w
	)

Frequency response of filter.

Author: Tony Ottosson

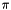Calculates the N-point frequency response of the supplied digital filter over the frequencies w. If w is not given the response is evaluated over the range 0 to $\pi$ with N values. The default value of N is 512.

If w is supplied polyval() is used. Otherwise the calculation is based on the fft.

Definition at line 136 of file filter_design.cpp.

References itpp::cos(), itpp::elem_div(), itpp::max(), itpp::polyval(), itpp::sin(), itpp::to_cvec(), and itpp::zero_pad().

vec itpp::polystab ( const vec & a )

inline

Polynomial Stabilization.

Author: Tony Ottosson

Stabilizes the polynomial transfer function by replacing all roots outside the unit cirlce with their reflection inside the unit circle.

Definition at line 56 of file filter_design.h.

References itpp::polystab().

cvec itpp::polystab ( const cvec & a )

inline

Polynomial Stabilization.

Author: Tony Ottosson

Stabilizes the polynomial transfer function by replacing all roots outside the unit cirlce with their reflection inside the unit circle.

Definition at line 58 of file filter_design.h.

References itpp::polystab().

Classes

Functions

Detailed Description

Function Documentation